CS2130:Section 5.1: Difference between revisions
Jump to navigation
Jump to search
(Create section 5.1) |
(add images) |
||
| Line 11: | Line 11: | ||
==== Into ==== | ==== Into ==== | ||
[[File:Into-set.svg|thumb|150x150px|A visual representation of the Into function]] | |||
Everything in A is used, and goes to only one element in B | Everything in A is used, and goes to only one element in B | ||
{{Clear}} | |||
==== Onto ==== | ==== Onto ==== | ||
[[File:Onto-set.svg|thumb|150x150px|A visual representation of the Onto function]] | |||
Everything in B is used | Everything in B is used | ||
{{Clear}} | |||
==== 1-to-1 ==== | ==== 1-to-1 ==== | ||
[[File:1-to-1-set.svg|thumb|150x150px|A visual representation to the 1-to-1 function]] | |||
Any element in B can go to <u>at most</u> one element in A | Any element in B can go to <u>at most</u> one element in A | ||
{{Clear}} | |||
==== Invertible ==== | ==== Invertible ==== | ||
''Also known as a bijection'' | ''Also known as a bijection'' | ||
[[File:Bijection-set.svg|thumb|150x150px|A visual representation of the Invertible/Bijection function]] | |||
Both 1-to-1 & onto | Both 1-to-1 & onto | ||
{{Clear}} | |||
== Symbols == | == Symbols == | ||
Latest revision as of 01:16, 24 January 2024
What is a function?
Unlike previous math classes, the Vertical Line Test is not used in this course
Terms
- Domain - Inputs of a function
- Range - Outputs of a function
Types of functions
Todo: add graphics to go along with these functions
Into
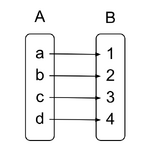
Everything in A is used, and goes to only one element in B
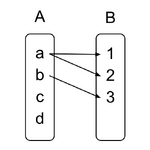
Onto
Everything in B is used
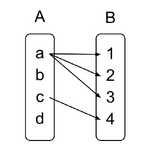
1-to-1
Any element in B can go to at most one element in A
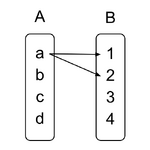
Invertible
Also known as a bijection
Both 1-to-1 & onto
Symbols
Negation
=
Unsure if this is the correct name
Everything in the Universe except what is inside A
Count Of
Count of elements inside A
Union
A combination of both sets
Intersection
A set containing what is in both sets
Element
is an element of
Subset
1 is a subset of
Notes
- The total number of subsets a set can have is equivalent to
Symmetric Difference
Everything in but not in
Effectively a unique filter
Example
Empty Set
An empty set
Notes
- An Empty Set is a Subset of any set, but not an element of every set
- An Empty Set is only an element of a set if explicitly a part of the set (you won't see this)













